数构与算法 | 什么是大 O 表示算法时间复杂度
正文:
开篇我们先思考这么一个问题:一台老式的 CPU 的计算机运行 O(n) 的程序,和一台速度提高的新式 CPU 的计算机运 O(n2) 的程序。谁的程运行效率高呢?
答案是前者优于后者。为什么呢?我们从时间复杂度分析就可以知道。
1、什么是时间复杂度?
在进行算法分析时,语句总的执行次数 T(n) 是关于问题的规模n 的函数,进而分析 T(n) 随 n 的变化情况并确定 T(n) 的数量级,算法的时间复杂度,也就是算法的时间度量,记作:T(n) = O(f( ))。它表示随问题的规模 n 的增大,算法的执行时间的增长率 f(n) 的增长率相同,称作算法的渐近时间复杂度,简称为时间的复杂度,其中 f(n) 是问题规模n的某个函数。
这样用大写 [ O( ) ] 来体现算法时间复杂度的记法,我们就称之为大O记法。例如:O(n)、O(1)、O(n2)、O(log n) 等等。一般情况下,随着 n 的增大,T(n) 增长最慢的算法为最优算法。
2、推导大O阶的方法
如何推导大O阶的表示方法,总结了三句口诀:
- 用时间1取代运算时间中的所有加法常数。
- 在修改后的运行的函数中,只保留最高阶项。
- 如果最高阶项存在且不是1,则去除与这个项相乘的常数。得到的结果就是大O阶。
说了太多文字显得太抽象,我们来看看一个例子你就明白了。
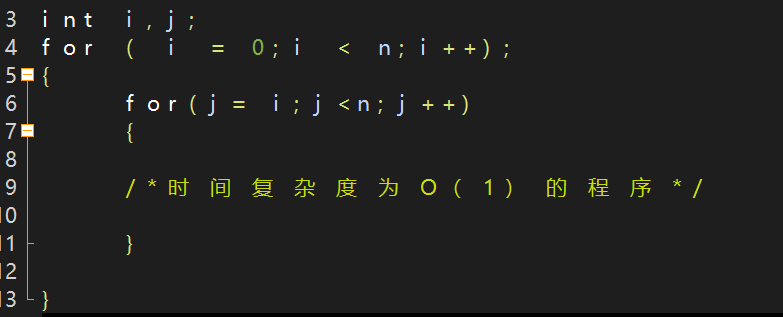
如图这个时间复杂度你知道是多少吗?
分析:
当 i = 0时,内循环执行了 n 次,
当 i = 1时,内循环执行了 n-1 次,
····
当 i = n-1时。执行了 1 次,所以总的执行次数为:n = (n-1)+(n-2)+ ··· + 1= n(n+1)/2 = n2/2+n/2。
由上面的公式可得:第一条代码中没有加法常数项,不考虑;第二条只保留最高阶项,因此保留 n2/2;第三条去除这个项相乘的常数,所以去除了 1/2;最终我们得到的代码段时间复杂度就是 O(n2)。
所以有了上面这个公式我们就可以对一般的时间复杂度大O的推导求解,其实理解大 O 推导不算难,难得是对数列的一些相关运算。更多的是考察你的数学功底。所以能不能写出好的高效率代码和你的数学功底有关哦。数学真的很重要(认真脸)。
3、一些常用的O( )时间复杂度推导
例1:O(1)常数阶
int sum = 0, n = 100; /* 执行一次 */
sum = (1+n) *n/2; /* 执行一次 */
printf(“the sum is:%d”,sum); /* 执行一次 */
我们可以看出运行次数的函数是 f(n) = 3。根据我们上面的大O阶公式 1 可以得到,把常数项 3 改为 1,在保留最高阶时发现没有最高阶项,所以时间复杂度为大 O(1)。也就是说,无论算法是 3 次还是 30 次,哪怕是 300 次,这些只要是常数项,它的时间复杂度都为大 O(1),而不是O(3)、O(30)、O(300)。即我们称之为常数阶。
例2:O(n)线性阶
从上面的这段代码我们可以看出,它的时间复杂度为O(n),因为循环体中的代码需要执行n次。
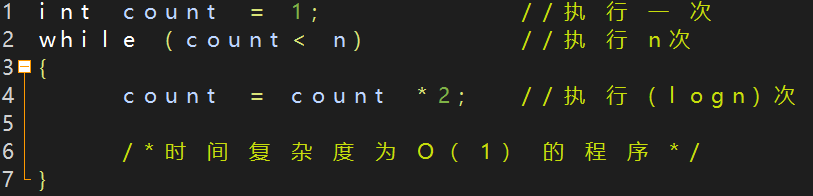
例3:O(log n)对数阶
上面代码我们可以看出,count = count * 2 之后就距离 n 更近里布,也就是说,有多少个 2 相乘后大于 n,就退出循环。所以我们可以由 2x = n 推导出 x = log2n ,像这样的循环时间复杂度,我们就称为对数阶的复杂度即为 O(log n)。
例4:O(n2)平方阶
这是有 2 个 for 语句组成的循环,是每一个循环代码执行 n次,所以整个代码就是 n*n 次,所以时间复杂度为 O(n2) 。
注意:如果外面的的循环次数不是 n 而是 m 那么时间复杂度就变为了 O(m*n) ,所以,循环的时间复杂度就等于循环体的的复杂度乘上该循环的运行次数。
数据结构中我们一般常用的时间复杂度表示有:O(1)、O(n)、O(n2)、O(log n)、O(nlog n)、O(n3)、O(2n)。
按时间复杂度所耗费的时间从大到小排序依次为:
O(1) < O(log n) < O(n) < O(nlog n) < O(n2) < O(n3) < O(2n)
到这里,我们就可以清楚的明白了开篇的问题,为什么老式 CPU 程序运行速率比新式的 CPU 运行效率高的原因就是应为O(n)< O(n2) 时间复杂度的关系,所以能写出好的算法是可以让计算机变得轻松的。
4、时间复杂度的三种情况
1.最好情况时间复杂度:
顾名思义,看名字你就知道,就是代码执行的次数为一次即为最好的 O(1)。这是要我们写代码最想要的。但是这是不现实的。
2.最坏情况时间复杂度:
同样的看名字你也可以知道,这是代码执行的总次数很多,每次都要运行 n 次,所以表示为 O(n)。这是我们写代码最不想要的。当然这也是不现实的。
3.平均时间复杂度:
就是把最好情况时间复杂度和最坏情况时间复杂度求取一平均值,这是我们写代码最有意义的,因为这是期望的运行时间,所以在写代码时应当考虑这一点。
5、算法空间复杂度
所谓算法的空间复杂度就是通过计算机算法所需求的存在空间实现。计算公式可以表示为:S(n) = O( f(n) ),其中,n为问题的规模,f(n) 为语句关于 n 所占存储空间的函数。
一般情况下,一个程序在机器上运行时,除了考虑到程序的本身运行指令,常数,变量和输入数据外,还需要考虑存储对数据操作的存储单元。
我们在写代码时完全可以用空间换取时间,两者不存在绝对的好与坏,这么用好二者关系取决于你用在什么地方。所以,实际情况还是要根据工程代码做最完美的选择。
6、总结
- 时间复杂度大O表示方法的由来。
- 大O推导的表示方法和常用的大O表示法时间复杂度。
- 时间复杂度的三种情况:最好情况、最坏情况和平均情况。
- 算法空间复杂度,适当情况可以用空间换取时间。
=====================(完)===================