#搜索策略 为什么要学习搜索策略？ 搜索策略看上去像是一种妥协，没有从问题的角度来设计算法，没有接触到问题的本质，而是从解的角度，用各种各样的方法遍历来找答案。 就像是数值分析一样，牺牲精确度换取速度。 不过对于复杂的问题来说，搜索策略往往可以加速问题的求解，或者方便地求解。从这个角度来看，研究搜索策略还是有必要的。 ##两种基本的搜索策略 在树结构中，有两种最基本的搜索策略，分别是深度优先搜索和广度优先搜索。 本质都是遍历，对于不同的问题具有不确定性，只是先后顺序不用而已。这里没什么好讨论的 ##优化的搜索策略 ###Hill Climbing Hill Climbing 是针对深度优先搜索的优化，利用到已知信息来决定下一步搜索，而不是按照排列顺序决定。 爬山法利用贪心方法确定搜索方向，对于当前节点的下一步探索节点，利用这些节点的代价值判断，取其中最小（或最大）的作为下一步搜索节点。 如何确定代价？最简单的方法就是从当前节点到该节点的路径的权重。 当然也可以用别的方法，比如说下面的例子 ####算法使用举例   (图片来自洛吉洲老师的课件) 可以看到使用这种搜索策略的确可以加速解的寻找，寻找的复杂度不再会随着存储结构的不同而改变，而是稳定一些了。 但是这种方法也有弊病。因为无法证明f(n)值越小，就能够越容易找到解，比如说： 情况1：  情况2：  第二种情况要想移动到正确的位置，只需要移动3步，而第一种情况则需要很多步。 从这点来看，f(n)并不能完全正确的描述当前节点与正确解的距离。 因此这个算法也是不稳定的。 ###Best-First Search Strategy Best-First算法基于广度优先搜索的顺序。 同样是对下一次可访问节点的信息进行比较后选择下一步搜索节点，同样是利用代价值来作为比较的依据，二者的不同之出在于，Best-First将所有的可探索的节点都拿出来进行筛选，这一次没有被选中的节点下一次仍然会被考虑，每探索一个新节点后获得的新的子节点也都会加入考虑集合当中，因此会使用堆来维护待比较节点。 Best-First的优点在于，它可以同时考虑所有的可探索节点，不像Hill Climbing 算法孤注一掷，没有退路，一条路走到尽头。 但这同样也是Best-First的缺点——因为需要始终考虑所有可探索节点，如果问题的规模很大，就需要消耗很多存储空间以及花很多时间来维护堆结构。 针对不同的问题，可以选择这两种不同的算法 ###Branch-and Bound Strategy Branch-and-Bound Strategy 与前两种算法是兼容的，它可以使用HC，也可以使用BF实现，主要取决于问题的种类。 分支限界的思想，简单来说，就是利用解的上下界信息来剪除不必要的树枝，以加速搜索的速度。 一般的操作是，先利用Hill Climbing算法迅速找到一个可行解，然后利用该可行解的代价作为上界，对于没有搜索到尽头的路径，只要其代价已经高于代价上界了，则断言这条路线一定不能够找到最优解，因此不会对该路径进行继续搜索。 ##A*算法及其思考 A*算法其实是一种特殊的分支限界算法。 为什么这么说呢？ 分支限界算法简单来说，就是先找到一个可行解，然后利用优化解<=可行解到性质，一旦遇到某个路径的代价已经大于已知可行解了，马上终止该路径的搜索，减少搜索的路径，也就加速了找到解的时间。 这里分支限界的核心思想在于寻找上界。 A*算法的不同之处在于，其上界并不是一个已经找到的可行解的代价，而是每个节点的估计代价值。 //TODO ###A*算法的具体实现 假设一次树搜索的中间状态  红线以内为已经完成探索的节点，蓝色点为待探索的节点集Q，n代表其中任意一个节点 如果是爬山法，则从第一个已探索节点开始，只会选择其子节点中代价较小的进行下一步探索。 如果是Best-First，则会为Q维护一个堆，选择堆中代价最小的节点进行下一步探索。 分支限界法需要利用前面两者先找出一个可行解，然后利用可行解来加速完成余下路径的排查 但是A*算法的不同之处在于，它定义了自己的代价函数。分支限界法中每个节点的代价就是简单的从父节点到该节点的路径权值 而A*算法则是利用该节点所在路径的一个总代价的估计值作为该节点的代价。其具体定义如下：  定义了满足以上性质的代价函数之后，利用以代价函数值为节点代价的Best-First进行搜索，可以做到： 只要找到目标节点，就可以保证当前路径就是最优解，从而直接结束搜索。 ###A*算法的本质的讨论与思考 如果没有理解该算法的本质的话，看到代价函数的定义之后可能会困惑：h(n)明明是虚构的，怎么就从虚构的信息推出了真实的信息了呢。 代价函数如何定义并不重要，重要在于其满足了下面的性质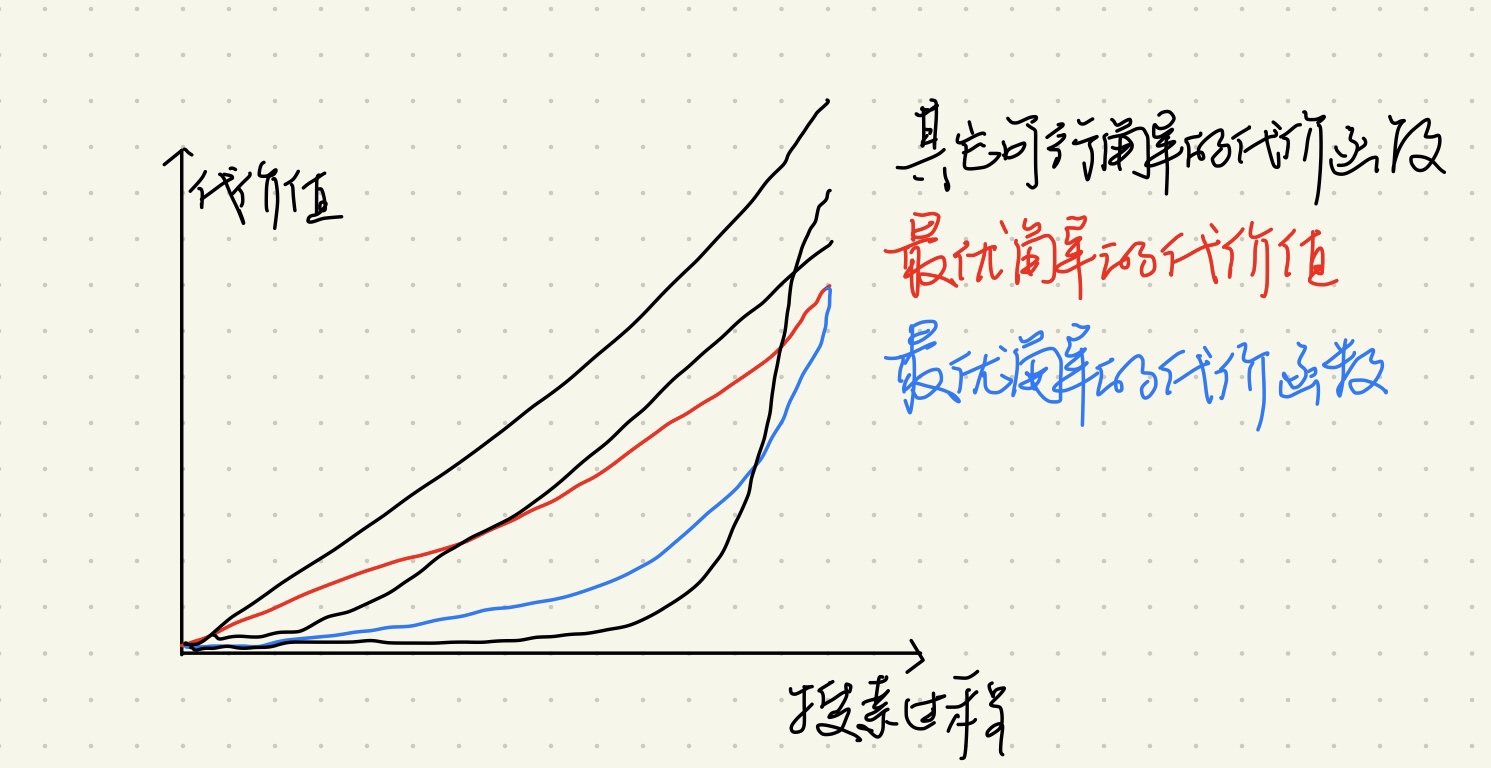：  1. 一旦搜索到目标节点，得到的代价函数值一定是真实的代价值 2. 搜索过程中，最优解的子路径的代价可能会比其他路径高，但是最终一定还是最优解的代价最低。 ####已发现的解一定是最优解，证明如下：  ###冷静一下 一步到位总归要付出代价。 A*算法的确很强，找到了解就可以放学回家了，不像普通的分支限界算法，还要辛苦的遍历余下路径。 但是并不代表A*的搜索路径就要少，因为它也可能需要走很多的路才会走到目标节点 考虑下面的极端情况  对于这样一个图，利用A*算法可能会产生下面的搜索过程：  可以看到，A*的性质保证了，一旦走到目标节点，得到的就是最优解，因此其它几次搜索都停在最后一步，无法越雷池一步。  但是也还是到了最后才搜索成功，实际上也已经基本上把图探索完了。 ##总结与思考 不可否认A*算法是一种更优化的算法，定义了代价函数之后的确会比一般的分支限界算法更有效率。思考一下。 最底层的搜索就是简单的遍历，更有效率的搜索会利用已知信息来决定下一步搜索的路径，差别在于利用的方法不同，策略也不同。 * 深度优先搜索与广度优先搜索是最基本的策略，没有利用任何信息，仅仅只是遍历的不同方式而已 * 爬山搜索(Hill climbing )一般用在深度优先搜索当中，利用当前节点的子节点的信息来决定下一步搜索 * Best-First Search Strategy则一般用于广度优先搜索，会利用所有节点的子节点的已知信息，不会闷死在一条路径上 * 分支限界是高于爬山与Best-First的策略，因为在执行分支限界的过程中会使用到这两种策略。分支限界相比前两者就聪明一些，剪除无效分支，树的大小是确定的，走的路少了，自然就要快一些 * 而A*是对分支限界对一种改进，用特殊的代价函数来替代代价，客观上可以加速搜索过程。 但是本质上而言，搜索策略终究还是蒙着眼睛走路，每一步都是猜测，都是根据经验或者已知来推测未知。 对于确定的场景，因为各自特点不同，所以选择不同的搜索策略的确能够提升效率，但是没有哪一种算法能够胜任所有情形，尤其是在我有意设计特殊的图来坑你的情况下。