简单聊聊红黑树（Red Black Tree）

âçº¢ä¸é»âçå¾çæç´¢ç»æ

前言

众所周知，红黑树是非常经典，也很非常重要的数据结构，自从1972年被发明以来，因为其稳定高效的特性，40多年的时间里，红黑树一直应用在许多系统组件和基础类库中，默默无闻的为我们提供服务，身边有很多同学经常问红黑树是怎么实现的，所以在这里想写一篇文章简单和大家聊聊下红黑树

小编看过很多讲红黑树的文章，都不是很容易懂，主要也是因为完整的红黑树很复杂，想通过一篇文章来说清楚实在很难，所以在这篇文章中我想尽量用通俗口语化的语言，再结合 Robert Sedgewick 在《算法》中的改进的版本（2-3树版本，容易理解也方便实现），可以保证让大家对红黑树的原理有大概的理解

其实对于大部分同学来说，大概了解红黑树的工作原理就基本够用了，因为通常不会有面试官让你去手写红黑树，你也几乎不需要去自己实现一个红黑树，看完这里，如果感觉意犹未尽，还有兴趣的同学可以去看看《算法导论》的红黑树实现，那是完整的4阶B树（2-3-4树）版本的实现

关于红黑树的主题，我们的文章有以下的灵魂三问：

为什么会有红黑树？
红黑树的应用场景和定义？
红黑树的高效和稳定是怎么实现？

为什么会有红黑树

要了解红黑树，先它的前辈：二叉树，平衡二叉树（我们的读者应该都具备这些前置知识，所以我们只做大概的讲解）

前置知识：

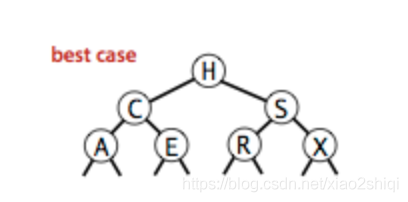
二叉树：传统的数组和链表等线性结构表效率低下，线性表在处理大规模数据的时间复杂度都是线性级别 O(n)，所以这种低效的数据结构，几乎不可能用来处理千万级别或者以上的数据量，于是基于二分思想的二叉树就诞生了，在最好情况下，二叉树查找的时间复杂度可以达到恐怖的对数级别 O(logN)，什么概念呢？就是在十亿级别的数据量里面，二叉树只需要15~30次的访问就可以找到目标，当然我们的前提是最好情况，那么最坏情况呢？可以参考下图

二叉树的最好/最坏情况：

上图可以看到，二叉树的性能的好坏，依赖数据的插入顺序，最坏情况下二叉树会退化为链表，所有操作的时间复杂度回到的线性级别 O(n)，那么怎么解决这个问题呢？

想要让树的查找效率最大化，那么就要保持树的平衡，所以平衡二叉树出现了，平衡二叉树的思想是在操作的时候对树进行平衡调整，来防止二叉树退化为链表，从而保证二叉树的最优查找性能，完美的平衡二叉树对高度的定义是相差不会大于1，这就相当于每次都插入/删除操作，都会对树进行平衡操作，这是代价非常高的操作，你可以理解为，类似数组为了保证有序性，数组中间插入数据，所有元素都要向后移动的代价，虽然名字叫平衡二叉树，其实它的性能非常不平衡，因为它是最大化插入/删除操作的时间来换取查找操作的时间最小化

看到这里，就有好奇的同学问，那么有没有既可以保证树的完美平衡，又可以保证所有操作性能的数据结构呢？可以很负责任的告诉你，有的，就是红黑树，我们先看看红黑树能为我们带来什么？

红黑树可以保证所有操作时间复杂度都是对数级别 O(logN)
和二叉树不同，无论插入顺序如何，红黑树都是接近完美平衡的
无数实验的应用证明，红黑树的操作成本比二叉树降低40%左右

常见树形结构的操作复杂度对比，可以看到红黑树是最均衡的：

âäºåæ çº¢é»æ æ¶é´å¤æåº¦âçå¾çæç´¢ç»æ

红黑树的应用场景和定义

简单罗列下我们常用的哪些工具是通过红黑树实现的

Java 的 HashMap （8 以后）的链表树化是通过红黑树实现
Java 的 TreeMap 是通过红黑树实现
Nginx 用红黑树管理 timer 等
Linux 进程调度用红黑树管理进程控制块
等等……

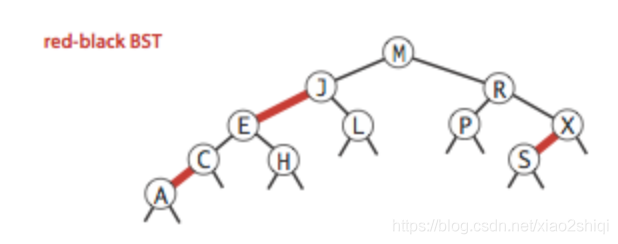
红黑树的定义，标准的红黑树示意图：

红黑树本身是二叉树，其背后的思想是使用二叉树的结构再加载额外的颜色信息，来表示2-3树，所以红黑树是包含了二叉树的高效查找和2-3树的高效插入平衡优点的算法

在我们讨论的版本中对红黑树的定义如下：

红链接必须为左链接
不能出现两条相连的红链接
该树是完美黑色平衡的

只看这些定义你可能会觉得描述非常的学院派，不好理解，我们先看看标准的红黑树，后面再用画图的方式来逐渐讲解

红黑树插入维护规则的核心代码

    private Node put(Node h, Key key, Value val) {
        // 二分插入
        if(h == null) return new Node(key, val, RED, 1);
        int cmp = key.compareTo(h.key);
        if(cmp < 0) h.left = put(h.left, key, val);
        else if(cmp > 0) h.right = put(h.right, key, val);
        else h.val = val;
 
        // 修复 右倾连接
        if(isRed(h.right) && !isRed(h.left)) h = rotateLeft(h);         // 违反规则 不允许出现右红连接
        if(isRed(h.left) && isRed(h.left.left)) h = rotateRight(h);     // 违反规则 不允许出现连续的左红连接
        if(isRed(h.left) && isRed(h.right)) flipColors(h);              // 当左右子节点为红色， 则变色
        h.size = size(h.left) + size(h.right) + 1;
        return h;
    }

红黑树的高效和稳定是怎么实现？

在插入数据的过程中红黑树会出现很多违反上面定义的情况，如果出现违反红黑树定义的情况，那么就依靠红黑树的三个核心操作来保证树的平衡，这三个操作也对应了红黑树定义的三条规则，分别如下：

左旋转（当出现右红子节点时，进行左旋转）
右旋转（当出现两条相连的左子红链接时，进行右旋转）
变色（当左右节点都是红链接时，进行变色）

左旋转

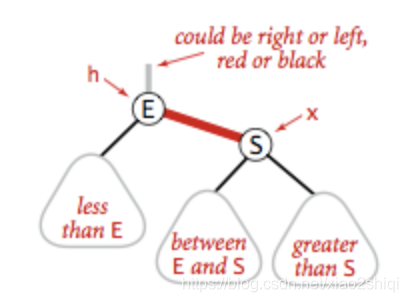
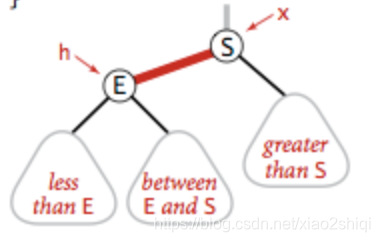
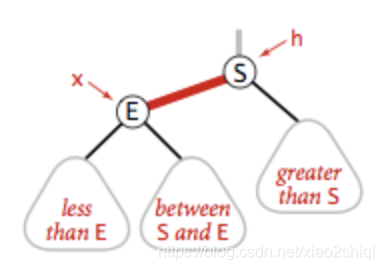
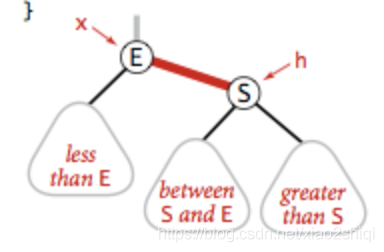
将红色的右节点，调整到树的左边，假如我要在树的底部插入元素S，但是元素被分配到的元素E的右边，具体如下：

左旋转是针对明显的红右链接，红色的右链接违反了红黑树定义的第一条规则，所以我们需要将它进行左旋转操作，被操作了左旋转后，元素E的位置会被元素S取代，E元素成为了S的左子节点，符合了二叉树的定义，左旋转的具体代码：

private Node rotateLeft(Node h) {
        Node x = h.right;
        h.right = x.left;
        x.left = h;
        x.color = x.left.color;
        x.left.color = RED;
        x.size = h.size;
        h.size = size(h.left) + size(h.right) + 1;
        return x;
    }

右旋转

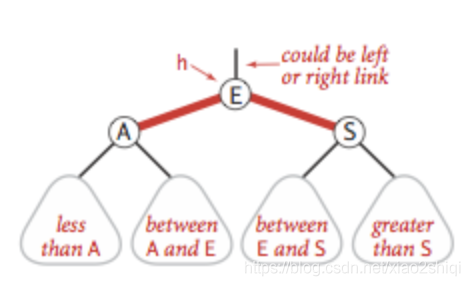
当左边出现连续的左红链接时，把左链接放到右边

右旋转的代码（右旋转的代码和左旋转几乎相同把 x.left 换成 x.right 即可）

private Node rotateRight(Node h) {
        Node x = h.left;
        h.left = x.right;
        x.right = h;
        x.color = x.right.color;
        x.right.color = RED;
        x.size = h.size;
        h.size = size(h.left) + size(h.right) + 1;
        return x;
    }

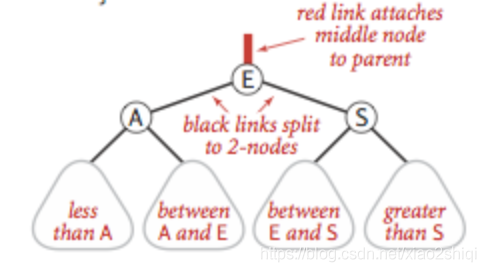
变色

当左右子节点都是红色的时候，把颜色进行转换，具体如图：

颜色转换的代码也非常简单：

private void flipColors(Node h) {
        h.color = !h.color;
        h.left.color = !h.left.color;
        h.right.color = !h.right.color;
}

理解了以上三种操作的原理，基本也就理解了红黑树的原理，有了这三种操作的基本知识，最后我们开始结合案例来分析红黑树插入平衡的全过程

为了便于理解，我们看一个简单的例子，下面罗列的三种情况：

插入最大键
插入最小键
插入中间键

我们可以发现，无论插入的数据如何不同，通过旋转，变色操作后最终得到的结果都是相同的，树永远保持平衡，具体可以看下方的示意图：

有了上面的理解，我们可以分析一组有序数据插入的过程，再结合文字逐步分析红黑树是怎么把它构造为一颗接近完美平衡的树

解析：

A首先成为根节点
C首先插入在A的右边，A违反了不能出现红右子节点的规则，进行左旋转，A成了C的左红子节点
E首先插入在C的右边，C违反左右子节点均为红色的规则，进行变色，C,A,E变黑（根节点永远为黑）
H首先插入在E的右边，E违反了不能出现红右子节点的规则，进行左旋转，E成了H的左红子节点
L首先插入在H的右边，H违反左右子节点均为红色的规则，进行变色，E,L变黑，H变红，导致C违反了不能出现红右子节点的规则，进行左旋转，C成为H的左红子节点（这里违反2个规则）
M首先插入在L的右边，L违反了不能出现红右子节点的规则，进行左旋转，L成为M的左红子节点
P首先插入在M的右边，M违反左右子节点均为红色的规则，进行变色，L,P变黑，M变红，导致H违反左右子节点均为红色的规则，进行变色，H,C,M变黑（这里违反2个规则）
R首先插入到P的右边，P违反了不能出现红右子节点的规则，进行左旋转，P成为R的左红子节点
S首先插入到R的右边，R违反左右子节点均为红色的规则，进行变色，S,P变黑，R变红，导致M违反了不能出现红右子节点的规则，进行左旋转，M成为R的左红子节点（这里违反2个规则）
X首先插入到S的右边，S违反了不能出现红右子节点的规则，进行左旋转，S成为X的左红子节点

通过以上证明，就可以得出结论，和二叉树不同，无论数据的插入顺序如何，红黑树都可以保证完美平衡

理解红黑树的背后思想，就能明白只要谨慎的使用简单的，左旋，右旋，变色这三个操作，就可以保证红黑树的两种重要的特性有序性和完美平衡性，因为旋转和变色都是局部操作，所以无需为整棵树的平衡性担心，另外红黑树的查找完全和二叉树相同，不需要额外的平衡，这里并不打算讲红黑树的删除操作，因为红黑树的删除实现复杂，比插入平衡还要复杂的多，要在文章里讲清楚很困难，推荐大家去看看我开篇推荐的经典书籍

总结

到这里对于为什么要使用红黑树的结论已经非常简单了，红黑树最吸引人的是它的所有操作在最好最坏情况下都可以保证对数级别的时间复杂度 O(logN)，是什么概念呢，可以简单说明对比下：

例如要在十亿级别的数据量找到一条数据，十亿的对数是30，线性表要找到数据需要访问十亿次，而使用红黑树的书只需要访问30次元素就能找到，10亿次/30次，差不多是3千万倍的性能提升，在现代上千亿数据的信息海洋里，只要通过几十次的比较就能随意的插入和查找数据，这是多么了不起的成就呀

而且对于二叉树，无数的实验和应用都能证明，红黑树的操作成本比二叉树要低 40% 左右（包含旋转和变色），红黑树自从被发现这40年来，一直高效稳定的通过各种应用的考验，包含需要系统基础组件和类库都是用红黑树，所以非常值得我们去学习和掌握它，最后留给大家一个问题，红黑树和散列表有什么区别，散列表查找的时间复杂度是常数级别 O(1)，那为什么很多场景我们不用散列表而用红黑树呢？欢迎留言拍砖

参考资料

https://algs4.cs.princeton.edu/33balanced/

https://algs4.cs.princeton.edu/33balanced/RedBlackBST.java.html

https://zh.wikipedia.org/wiki/%E7%BA%A2%E9%BB%91%E6%A0%91

https://book.douban.com/subject/10432347/

本文链接：https://www.cnblogs.com/xiao2shiqi/p/11301052.html

简单聊聊红黑树（Red Black Tree）

简单聊聊红黑树（Red Black Tree）的更多相关文章

随机推荐

热门专题

目录导航