连通图和连通分量  

1．顶点间的连通性
  　  在无向图G中，若从顶点vi到顶点vj有路径(当然从vj到vi也一定有路径)，快看小说网则称vi和vj是连通的。

2．连通图
    　若V(G)中任意两个不同的顶点vi和vj都连通(即有路径)，则称G为连通图(Con-nected Graph)。
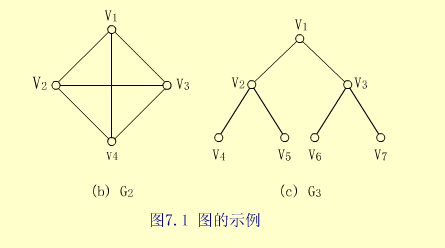
【例】图G2，和G3是连通图。
   
     ​
3．连通分量
    　无向图G的极大连通子图称为G的最强连通分量(Connected Component)。
  注意：
　　① 任何连通图的连通分量只有一个，即是其自身
    　② 非连通的无向图有多个连通分量。
  【例】下图中的G4是非连通图，它有两个连通分量H1和H2。
          ​

强连通图和强连通分量

1．强连通图
　    有向图G中，若对于V(G)中任意两个不同的顶点vi和vj，情定三生：首席医少赖上门都存在从vi到vj以及从vj到vi的路径，则称G是强连通图。

2．强连通分量
    　有向图的极大强连通子图称为G的强连通分量。
注意：
    　① 强连通图只有一个强连通分量，即是其自身。
    　② 非强连通的有向图有多个强连分量。
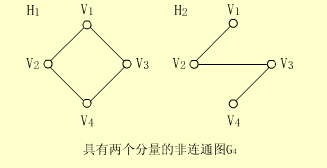
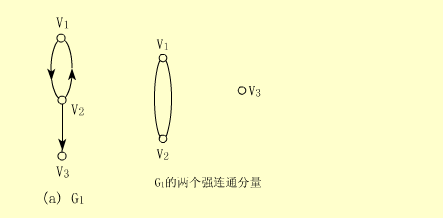
【例】下图中的G1不是强连通图，因为v3到v2没有路径，但它有两个强连通分量，如右图所示。

              
​
网络(Network)

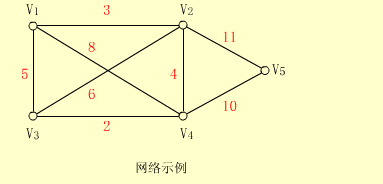
　    若将图的每条边都赋上一个权，则称这种带权图为网络(超级人生)。
注意：
　    权是表示两个顶点之间的距离、耗费等具有某种意义的数。

 

　　【例】下图就是一个网络的例子。

 

​

　　　　　　　　　　 

版权声明：本文为Katerina原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://www.cnblogs.com/Katerina/p/11336043.html