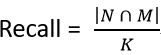一文纵览向量检索
摘要:本文针对向量检索要解决的问题,梳理了主流向量检索相关的技术,分析了向量检索目前的一个趋势。
什么是向量检索
首先我们了解下什么是向量,所谓向量就是由n个数字(二值向量由n个比特组成)组成的数组,我们称之为n维向量。而向量检索就是在一个给定向量数据集中,按照某种度量方式,检索出与查询向量相近的K个向量(K-Nearest Neighbor,KNN),但由于KNN计算量过大,我们通常只关注近似近邻(Approximate Nearest Neighbor,ANN)问题。
向量度量
常见的向量度量有四种:欧式距离、余弦、内积、海明距离
不同的度量方式对应不同的场景,通常欧式距离用于图片检索,余弦用于人脸识别,内积多用于推荐,海明距离由于向量比较小,通常用于大规模视频检索场景。
有了度量以后,我们通常会用召回率(也通常叫精度)来评估向量检索的效果,对于给定的向量q,其在数据集上的K近邻为N,通过检索召回的K个近邻集合为M,则
召回越接近100%代表索引效果越好。
向量检索解决的问题
向量检索从本质上讲,其思维框架和传统的检索方法没有什么区别,后面在讲解向量检索的索引结构部时,体会能更深刻一些。
1. 减少候选向量集
和传统的文本检索类似,向量检索也需要某种索引结构来避免在全量的数据上做匹配,传统文本检索是通过倒排索引来过滤掉无关文档,而向量检索是通过对向量建立索引结构来绕过不相关的向量,本文重点讨论相关的向量索引结构。
2. 降低单个向量计算的复杂度
传统文本检索在排序时通常会采用漏斗模型,上层计算比较轻量,越往下计算越精细,但随着过滤的进行,需要计算的文档数也逐级下降,对高维向量而言,单个向量的计算量还是比较重,通常会对向量进行量化,对向量做近似计算,最后在一个很小的数据集上做原始向量的排序。
下面我们围绕这两个问题来展开向量检索的相关讨论。
向量检索索引结构
为向量建立高效的索引结构是向量检索面对的头号问题,在开始展开前我们看一个Benchmark项目,这个项目在多个公开的向量数据集对比了相关索引结构的召回性能指标,使我们能够快速对各种索引结构的性能表现有个直观的认识。
暴力计算
暴力计算是最简单但复杂度最高的一种方式,在计算召回的时候,暴力计算的结果是作为答案的基准数据,在人脸识别的场景中经常要求100%的召回率,这种情况下一般直接暴力计算。
基于树的方法
基于树的方法有很多种,比较典型的有KDTree、BallTree、VPTree,类比传统的二叉树,树结构无非是在建树的时候是决定往左还是往右扩展,不同的向量树索引在于按照什么标准去决策,KDTree(如下图所示)会选取向量中某个方差最大的维度取中值作为判定标准,也就是以超平面去划分空间,而BallTree则以球面去划分空间,VPTree会先选取一个制高点,然后计算每个点和制高点的距离,取距离中值作为判定标准。通常这些方法在检索的时候都会利用三角形不等式来去除不必要的探索。
基于树的方法还有很多其他类型,但万变不离其宗,无非就是按照某个判定标准,对向量空间进行划分,但不管怎么划分,由于需要回溯的,都决定了基于树的方法在性能上要稍逊一筹。
哈希方法
哈希对大家再熟悉不过,向量也可以采用哈希来加速查找,我们这里说的哈希指的是局部敏感哈希(Locality Sensitive Hashing,LSH),不同于传统哈希尽量不产生碰撞,局部敏感哈希依赖碰撞来查找近邻。
满足如下两个条件的哈希函数称为(d1,d2,p1,p2)-sensitive:
1. 如果d(x,y) <= d1,则h(x) = h(y)的概率至少为p1;
2. 如果d(x,y) >= d2,则h(x) = h(y)的概率至少为p2;
上面的表达式用人话来说就是:高维空间的两点若距离很近,那么设计一种哈希函数对这两点进行哈希值计算,使得他们哈希值有很大的概率是一样的,若两点之间的距离较远,他们哈希值相同的概率会很小。不同距离度量的哈希函数不同,不是所有距离度量(如内积)都能找到对应局部敏感哈希
基于倒排方法
传统倒排索引是根据文档包含某个词,然后将当前文档放入改词的倒排索引中来建立索引结构,那向量是如何建立起倒排索引呢?通过聚类把整个向量空间划分为K个区域,每个区域用一个中心点C代替,这样每个向量和所有中心点对比,将自身归入到距离自己最近的中心点对应的倒排,整个索引结构就建立起来了
另一种基于倒排的索引是BOW,原理大体相同,例如一张图片会抽取出几百个局部特征,先对所有的特征聚类,形成中心点,这些中心点作为倒排的基础,建立索引时,把图片的每个局部特征归类到其最近的中心点,建立倒排,检索时会根据命中的次数来过滤结果。
基于图的方法
前面介绍的索引结构都可以归类为基于空间划分的方法,每个向量只会属于某个划分好的一个区域,这些方法最大的的问题是为了提高召回需要考察很大一块区域的向量,导致计算量激增,那有没有更好的方法来解决这个问题呢?基于图的方法就可以比较好的实现这一目标,图方法最朴素的想法是邻居的邻居也可能是邻居,这样把最近邻的查找转化为图的遍历,由于其连通性,可以针对性的考察部分向量而不是按区域来考察,因此可以大幅降低向量的考察范围。
最近几年图方法是向量检索研究的一个热点,出现了如KGraph、NSG、HNSW、NGT等一批图索引方法,但实际上这些图方法的主要区别在构建过程,不同图方法采用不同的手段来提升图的质量,但图检索的步骤基本是一致的:a.选好入口点;b.遍历图;c.收敛。在不断实践中我们观察到一些特性来评判图索引质量,指引我们在图方法改进的方向:
1. 邻居点接近K近邻
2. 邻居点数量尽可能少,即减少出度
3. 尽可能保证图的连通性,增加入度
下面我们以HNSW为例介绍一下图方法的原理,之所以选取HNSW在于该方法易于理解,比较容易实现流式索引构建和更新,属于传统方法在向量上的完美体现。
HNSW背后其实是跳表在图上的应用,跳表作为一种简单高效的索引结构在Redis、LevelDB等系统中获得广泛应用,如下图所示:
第一层上有全量的数据,在上层根据随机投币决定,越往上投到的概率越小,投到高层的节点往下都有一条记录,作为检索的高速公路快速前进。
HNSW的原理也类似,不同于传统跳表在每层用链表来串联节点,HNSW在每层都是一个NSW(Navigable Small World Graph),通过图数据结构组织,上层节点也是通过投币决定在哪一层,并且它们在下层图中都有记录,上层图可以看做下层图的一个缩影,检索时,从上到下,不断指引检索过程逐步靠近想要探寻的向量空间。另外在构图过程中HNSW通过边的裁剪来保证图的连通性,这里顺便提一下,纵观多篇图方法的论文,都从自己的视角表述了边裁剪方法, 但不管各种方法对裁边描述的有多酷炫,其方法本质都是一模一样的,只是视角不一样而已。
向量量化
前面把主流的向量检索的索引技术基本都概述了一遍,经过索引结构对考察的向量做了裁剪以后,对高维向量而言,单个的计算量还是很大,有没有方法来减少计算量呢?量化正是基于这个目的技术,所谓量化是指把一个很大的值空间量化到一个较小的值范围,举个简单的例子,全世界有60多亿人口,也就是地球人的表征有60多亿种,我们可以把人量化为男人和女人两种类型,这样就把一个60多亿的空间量化成只有两个值的范围。
常用的量化一般包括PQ(及其优化OPQ、LOPQ)和二值两种。
PQ原理如图,PQ中的P是乘积的意思,那怎么就冒出个乘积呢?在下图中一个128维的向量空间在经过PQ处理后,向量空间切分成了4段,每段内由256个中心点来量化表达,因此原始的128维空间现在可以用每段里的中心点组合,也即256 * 256 * 256 * 256种组合来表达,这就是所谓的乘积。
对于二值向量,由于现代CPU都提供了专门的指令,计算海明距离非常快速,在海量的向量检索中通常会直接生成二值向量,生成二值向量方法常见的有ITQ(Iterative Quantization)、DeepHash等方法。
其他技术
聚类
向量聚类主要指的是K-means系列方法,如经典的K-means、K-means++、K-means#、One pass K-means、YinYang k-means等,在实践中我们也使用过分层的方法来获得海量中心点。
内积转换
前面在哈希章节我们已经看到对内积是没有办法找到对应的局部敏感哈希函数,内积也不满足三角形不等式,因此导致很多索引结构无法直接使用内积作为度量,大多数做法是先对向量做归一化再检索,但归一化会转换向量空间分布。研究人员通过一个数学观察发现了一个方法,通过一定规则变换,可以使得内积和欧式能够实现负相关,如下图所示:
对向量转换后,可直接用欧式距离度量方式检索。
向量检索发展趋势
本文开头我们提到向量检索的思维框架和传统检索没有什么区别,到目前为止传统方法应用到向量检索的红利也基本吃完。这两年的一个发展趋势是各种方法的组合,通过吸收各种方法的长处,来获得更好的性能、承载更大规模的向量。
量化图
从Benchmark上我们可以清晰的看到,处在优势地位的方法基本被图方法霸屏,同时我们知道量化可以降低单个向量的计算量,因此很自然的一种想法是让两者强强联手,在图遍历过程中使用量化计算来加速,这种方法对于在高维度方法上优势明显,加速比能达到三倍以上。
图+倒排
图的性能虽然卓越,但缺点也非常明显,为了保证检索效果,图上边的保存消耗大量的存储
尤其在向量本身很小的二值向量上,这是不能承受之重,另外图的邻居本身具有随机性,对硬件处理向量也非常不利。倒排方式则恰恰相反,索引结构基本不消耗太多空间,但缺点是空间划分方法容易导致召回率不高,但我们从暴力计算的观察获得一些启发,暴力计算从空间划分角度有两种视角:可以将暴力计算看做成把所有向量聚类为一个;也可以将暴力计算看做聚类为N(N为向量数据集的大小)个中心,每个中心点是向量本身。这两种方法都能100%召回,但他们一个是因为中心点下面的向量太多,另一个因为聚类的中心点太多,而导致计算量不可接受,那我们是否可以找到一个平衡点?适当的中心点数目使得召回和性能取得一个比较好的平衡?图+倒排方式应运而生,用海量中心点去分割向量空间,图方法来组织海量中心点。
华为云向量检索实践
向量检索的应用出现了空前的繁荣,华为云搜索服务(Cloud Search Service,CSS)目前已经对外开放向量检索的能力,我们针对高性能和海量数据两种典型的场景都提供了解决方案。
实现上我们主要基于图方法,在裁边优化,连通性增强,指令加速,多线程处理等方面做了大量增强。对比测试中,我们召回率远高于Faiss,在高维度数据上差距更为明显,在同样召回下,我们性能在SIFT,GIST等公开数据集上是Faiss 2.3倍以上。对比测试采用的是相同的机器,相同的算法。
总结:
本文针对向量检索要解决的问题,梳理了主流向量检索相关的技术,分析了向量检索目前的一个趋势。在向量检索的发展历程中,还有很多相关的方法没有囊括进来,但万变不离其宗,这些方法要么还是传统方法的扩展或者应用三角不等式的优化或者应用层次方法等等。期盼本文能帮助梳理向量检索的脉络。
参考文献:
1. J. L. Bentley. Multidimensional binary search trees used for associative searching. Communications of the ACM, 18:509–517,1975
2. P. N. Yianilos. Data structures and algorithms for nearest neighbor search in general metric spaces. In Proc. of the 4th annual ACM-SIAM Symposium on Discrete Algorithms, pages 311–321, 1993
3. Liu, T.; Moore, A. & Gray, A. (2006). New Algorithms for Efficient High-Dimensional Nonparametric Classification. Journal of Machine Learning Research. 7: 1135–1158.
4. P. Indyk and R. Motwani. Approximate nearest neighbors: Towards removing the curse of dimensionality. In STOC, pages 604–613, Dallas, TX, 1998.
5. W. Dong, C. Moses, and K. Li. Efficient k-nearest neighbor graph construction for generic similarity measures. In Proceedings of the 20th international conference on World wide web, pages 577–586. ACM, 2011.
6. Y. A. Malkov and D. A. Yashunin. Efficient and robust approximate nearest neighbor search using hierarchical navigable small world graphs. CoRR,abs/1603.09320, 2016.
7. https://arxiv.org/abs/1707.00143
8. https://yongyuan.name/blog/vector-ann-search.html
9. A. Shrivastava and P. Li. An improved scheme for asymmetric lsh. Technical report, arXiv:1410.5410, 2014.
10. H. Jegou, M. Douze, and C. Schmid. Product quantization for nearest neighbor search. IEEE transactions on pattern analysis and machine intelligence, 33(1):117{128, 2011.
11.https://arxiv.org/abs/1810.07355
注:本文部分索引结构示例图源自https://yongyuan.name/blog/vector-ann-search.html