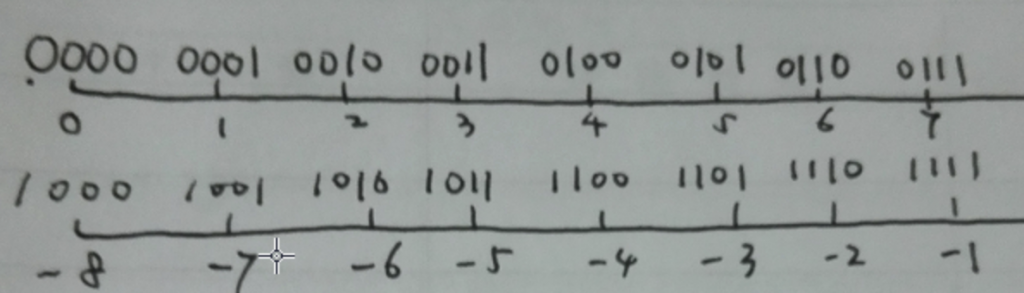简简单单理解原码、反码和补码
这些个概念,大学是肯定学过,当然了大学基本为了应付考试,然后我考试又是长期抄我上一桌的同学,所以你懂的。。毕业工作后也专门去看了这些个概念,不过之前的学习并没有摸透,可能因为没有理解也容易忘,这次是想好好学习下计算机组成原理,又遇到了原码,反码,补码这些玩意儿,结果看了下网上的文章,自己也在本子上画画写写,有了一些总结,就赶紧记录下来。
原码计算的问题
计算机的运算器中是没有减法运算器的,大概的原因是减法运算器开销太大,就放弃了,所以计算机就没法直接做减法而是要通过加法来实现减法的功能,比如:
5 - 3 = 5 + (-3) = 2;
然后我们用原码来分别对正数,负数进行计算,因为都用加法所以就引入了符号位用来表示正负数,即第一位为1代表负数为0代表正数。若以带符号的4位二级制来进行计算,如下:
1 + 3 => 0001 + 0011 = 0100 = 4 [结果正确]
5+(-3) => 0101 + 1011 = 10000 = 0000(高位溢出舍弃) [结果错误]
(-1)+(-1) => 1001 + 1001 = 10010 = 0010(高位溢出舍弃) [结果错误]
可以看到用原码进行计算除了正数相加外其他都会有莫名其妙的结果,而且用原码因为有符号位的问题,0就存在-0(1000)跟0(0000)两种表示方法,于是就有了补码。
补码真香
要理解补码,我们要先看一个时钟的计算
要将时钟的7点转到10点,我们可以逆时针转9下,或者顺时针转3下,即对于有限位数的计算(时钟上的数最大到12)我们得到了如下公式:
7 - 9 = 7 + 3 = 10;
所以对于时钟计算来说12就称之为模,超过12就得从1重新开始计算,类似二进制的高位溢出,其中-9跟3称为12的同余数。
如何理解这个同余数呢,其实正数的同余数非常好理解,就是基于某一个数余数相同的数,比如这边的时钟最大就是12,基于12余数为3的正数有哪些呢,3,15,27 … 可以看到,如果以时钟的顺时针方向代表加1,逆时针代表减1,那往正数取同余数就是绕这时钟顺时针方向一圈一圈的绕,3顺时针绕一圈是15,再绕一圈是27,由此我们可以推出负数的同余数就是绕着时钟逆时针一圈一圈的绕,结果为-9(3-12,逆时针绕一圈),-21(-9-12,逆时针再绕一圈), -33(-21-12) … 所以上边的公式我们也可以写成这样
... 7 - 21 = 7 - 9 = 7 + 3 = 10 = 7 + 15 = 7 + 27 ...;
说白了无非就是多转几圈而已,通过对同余数的理解,我们得出这样一个结论,新航道学校对于有限制的位数的计算(时钟上的数最大到12),我们减去一个数,可以等同于加上他的同余数,成功将减法转换成了加法运算。我们将这个结论应用到2进制计算中来。
我们依然用4位2进制来举例,我们先不引入符号位,则4位2进制如下
因为1111+1=10000,最高位溢出,其结果为0000,从而又回到了0,从头开始,其实溢出就是上边的时钟的转完一圈重新开始的意思,高位溢出能够舍弃也是因为转完一圈后从头开始算并不会影响最终的结果。我们来具体计算下
5-2 = 0101(5)-0010(2) = 0101+(-0010) = 0101(5)+1110(14) = 10011 = 0011(3)
4位2进制的模是16,即总的能代表的数是16个数,也可以说一圈就是16个数,所以参考上边时钟的例子,减去2既可以通过逆时针后退2格,也可以通过顺时针前进14格来计算,即-2与14基于16来说是同余数。我们成功的将二进制的减法转换成了加法,同时我们把这里的1110(14)叫做-0010(-2)的补码。因为正数可以直接参与计算所以正数的补码还是自己,所以我们得到了下边的公式
[x]原 - [y]原 = [x]原 - [y]原 + 模 = [x]补 + [y]补
通过补码成功的解决了原码带来的符号位计算的问题,引入补码后4位2进制表示的范围不再是0~14 而是-8~7,如下图
你可能注意到,补码是不存在0(原码0000)与-0(原码1000)的说法,因为2个相反的数通过补码来运算只会得到0000,比如0111(7)+1001(-7)=0000,所以把补码1000人为的规定为-8.可能也因为最高位为1,所以归到-8比较合理。
通过反码用来计算补码
大学的课本,或者网上算补码的方式,都是说正数的原码,反码,补码一致,负数的补码等于反码加1,雅思考试时间为什么负数的补码是等于反码加1呢?我们慢慢来推导。
通过上边的钟表我们可以通过顺时针走多少格来计算负数的补码,但是对于位数非常多的二级制,比如32位,64位,我们不可能通过画类似的时钟来算补码,所以我们就得有个公式能够非常方便的计算出补码,这时候反码就应运而生了。
我们从上边计算补码的公式中知道,对于负数的补码
[y]补 = [y]原 + 模 (y<0)
以上边的4位2进制来解释这个公式
[1010(-2)]原 = [1110(14)]补 = [1010(-2)]原 + [16]模
同时我们知道模就是溢出,所以 [ 模 = 1111 + 1 ] 于是上边的公式就转为
[1010(-2)]原 = [1110(14)]补 = [1010(-2)]原 + [16]模 = [1010(-2)]原 + 1111 + 1
综上,我们把 [1010(-2)]原 + 1111 称为反码,因为要计算一个数与另一个数的结果为1111是非常容易的,只需符合位不变,其余求反即可,1010 -> 1101。再通过上边的推导公式,将反码加1就得到了补码,1101+1->1110。通过上边的推导我们知道了为什么补码是等于反码加1。
其实还有另个更快的计算补码的小窍门,对于负数的原码,保留原码的符号位,然后从右往左开始,直到遇到1之前都保持不变(包括遇到的第一个1),其余取反,如下,[]框起来的是不变的,加粗是取反的
1010 -> [1] 1 [10] ->1110
11010000 -> [1] 01 [10000] ->10110000