统计学基础知识
统计学基本知识
1、总体和样本基本概念：
(1) 总体:表示研究对象的整个群体。
(2) 样本:表示从总体中选取的一部分。
2、总体方差和样本方差：
(1) 定义：
总体方差：总体方差是一组资料中各数值与其算术平均数离差平方和的平均数
公式为：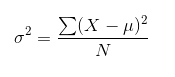
样本方差：样本方差是指构成样本的随机变量对离散中心 x之离差的平方和除以n-1，样本方差用来表示一列数的变异程度
公式为：
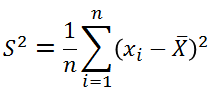
(2) 区别：总体方差是个确定值，样本方差是个随机变量
3、随机变量：
随机变量与普通变量不同，因为随机变量通常是一个函数，用于量化随机过程。通常用大写字母X，Y，Z等表示，而传统变量通常用小写字母x，y，z表示。随机变量有两类：离散型和连续型。
4、泊松分布：
(1) 定义：泊松分布是一种统计与概率学里常见到的离散概率分布。
(2) 公式：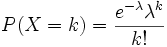
泊松分布P (λ)中只有一个参数λ ，它既是泊松分布的均值，也是泊松分布的方差。其中k=0,1,2…
正态分布
上面表达式中有两个参数，即期望（均数）μ和标准差σ，σ2为方差
当μ = 0,σ = 1时的正态分布是标准正态分布。
大数定律
举个例子: 投硬币
一枚硬币被抛出后有50%的可能为正面或者背面，在小样本的情况下，随机抛硬币的结果可能并不明显或者说结果没有规律，不稳定等等，10次里可能有4次正面6次背面，也可能是7次正面3次背面，这很正常。但是随着我们抛硬币的次数的增多，正面和反面出现次数就会越来越接近于相同，也就是各趋近于50%。
版权声明：本文为zhgmen原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。